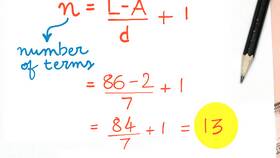Прогрессии - числовые последовательности с определенным законом изменения элементов. Рассмотрим методы нахождения суммы для арифметической и геометрической прогрессий.
Содержание
Арифметическая прогрессия
Последовательность, где каждый следующий член отличается от предыдущего на постоянную величину (разность d).
Формулы для расчета суммы
| Формула | Применение |
| Sₙ = (2a₁ + d(n-1))n/2 | Через первый член и разность |
| Sₙ = (a₁ + aₙ)n/2 | Через первый и последний члены |
Пример расчета
- Дано: 3, 7, 11, 15,... (n=10)
- a₁ = 3, d = 4
- Используем первую формулу: S₁₀ = (2*3 + 4(10-1))10/2 = (6 + 36)*5 = 210
Геометрическая прогрессия
Последовательность, где каждый следующий член получается умножением предыдущего на постоянное число (знаменатель q).
Формулы для расчета суммы
| Формула | Применение |
| Sₙ = a₁(1 - qⁿ)/(1 - q) | Для q ≠ 1 |
| Sₙ = a₁n | Для q = 1 |
| S = a₁/(1 - q) | Для бесконечной прогрессии при |q| < 1 |
Пример расчета
- Дано: 5, 10, 20, 40,... (n=5)
- a₁ = 5, q = 2
- Используем формулу: S₅ = 5(1 - 2⁵)/(1 - 2) = 5(1 - 32)/(-1) = 155
Сравнение прогрессий
| Характеристика | Арифметическая | Геометрическая |
| Закон изменения | Прибавление d | Умножение на q |
| Сумма n членов | Линейный рост | Экспоненциальный рост |
| Бесконечная сумма | Не существует | Сходится при |q| < 1 |
Практические советы
- Определите тип прогрессии по первым трем членам
- Выявите параметры: a₁, d или q
- Выберите подходящую формулу
- Проверьте корректность подстановки значений
- Для больших n используйте калькулятор
Типичные ошибки
- Путаница между формулами разных прогрессий
- Неправильное определение знаменателя q
- Использование формулы бесконечной суммы для конечного случая
- Ошибки в знаках при отрицательных d или q
Понимание методов расчета суммы прогрессий позволяет решать широкий круг математических и прикладных задач в экономике и физике.