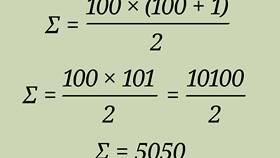В математике часто встречаются задачи, требующие доказательства равенств с удвоенными суммами. Рассмотрим несколько типичных случаев таких доказательств и методы их решения.
Содержание
Основные случаи удвоенных сумм
| Тип суммы | Пример выражения |
| Арифметическая прогрессия | 2(a₁ + a₂ + ... + aₙ) = n(a₁ + aₙ) |
| Геометрическая прогрессия | 2(b₁ + b₂ + ... + bₙ) = b₁(1 - qⁿ)/(1 - q) |
| Квадраты чисел | 2(1² + 2² + ... + n²) = n(n+1)(2n+1)/3 |
Методы доказательства
Метод математической индукции
- Проверить базис (n=1)
- Предположить верность для n=k
- Доказать для n=k+1
- Сделать вывод
Метод перегруппировки слагаемых
Пример для суммы первых n натуральных чисел:
- S = 1 + 2 + ... + n
- 2S = (1+n) + (2+(n-1)) + ... + (n+1)
- 2S = n(n+1)
- Следовательно, S = n(n+1)/2
Пример доказательства
Доказательство равенства для суммы квадратов
Докажем, что 2(1² + 2² + ... + n²) = n(n+1)(2n+1)/3
| Шаг | Действие |
| 1 | Проверим для n=1: 2·1²=2 и 1·2·3/3=2 |
| 2 | Предположим верность для n=k |
| 3 | Докажем для n=k+1 |
| 4 | 2Sₖ₊₁ = 2Sₖ + 2(k+1)² |
| 5 | Подставим предположение индукции |
| 6 | Упростим выражение |
| 7 | Получим требуемую формулу |
Применение в различных областях
- Анализ алгоритмов (вычислительная сложность)
- Теория вероятностей (математические ожидания)
- Физика (расчеты энергий)
- Экономика (финансовые расчеты)
Особые случаи
Для некоторых сумм удвоенное значение может быть представлено в виде:
- Произведения количества слагаемых на сумму крайних членов
- Интеграла от соответствующей функции
- Значения производящей функции в особой точке
Графическая интерпретация
Многие удвоенные суммы можно представить графически как:
- Площадь прямоугольника составленного из двух одинаковых фигур
- Симметричное расположение точек на координатной плоскости
- Диаграммы Эйлера-Венна для множеств